
A guide to understanding similarity search (also known as semantic search), one of the key discoveries in the latest phase of AI.
One of the key discoveries in the latest phase of AI is the ability to search for and find documents based on similarity search. Similarity search is an approach that compares information based on its meaning rather than via keywords.
Similarity search is also known as semantic search. The word semantic refers to the “meaning or interpretation of words, phrases or symbols within a specific context.” With semantic search a user can ask a question such as “What is the movie where the protagonist climbs through 500 feet of fowl smelling s*&t?” and the AI will respond with “The Shawshank Redemption”. Performing this kind of search is impossible with keyword searching.
Semantic search opens up all sorts of possibilities, whether for researches trying to find specific information out of university collections, or giving developers access to precise information when querying API documentation.
The genius of semantic search is we can convert entire documents and pages of text into a representation of its meaning.
The purpose of this article is to provide the fundamentals of semantic search, and the basic mathematics behind it. With a deep understanding, you can take advantage of this new technology to deliver highly useful tools to users.
The key to this technology is mathematics of vectors.
Vectors
You may recall from high school of university the concept of vectors. The are used reguarly in physics. In physics a vector is defined as a magnitude plus a direction. For example the car is travelling 50 km/hr north.
A vector can be represented graphically:

Vectors have a different meaning in Artificial Intelligence which we will come to shortly. I will talk you through how we get from a vector in Physics to a vector in AI.
Going back to our graphical representation, if we were to plot this in a graph we can represent a vector in 2-dimensions.
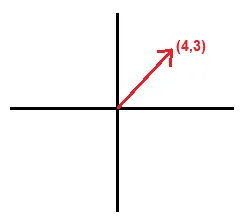
The end of the vector can be represented by its values on the x-axis and y-axis. This vector can be represented by the point [4, 3].
With this point we can use trigonometry to calculate it’s magnitude and direction.
If we create a vector in 3-dimensions we need three values to represent that vector in space.
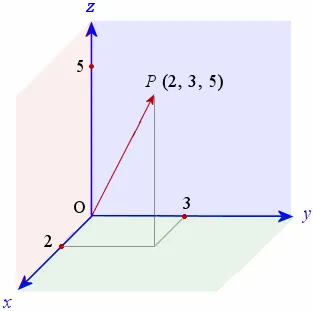
This vector is represented by the point [2, 3, 5]. Again we can apply trigonometry to calculate the magnitude and direction.
One of the interesting calculations we can perform with vectors in 2 or 3 dimensions is to determine the similarity between vectors.
In Physics one of the calculations we need to perform is vector similarity (this is leading to AI similarity search). For example in the study of materials science, vectors can be used to compare stress or strain vectors within materials under load.
In the diagram if we had stress vectors that were similar we could see that the strain on the material is in the same direction. Whereas opposite forces would apply a particular stress to the material.
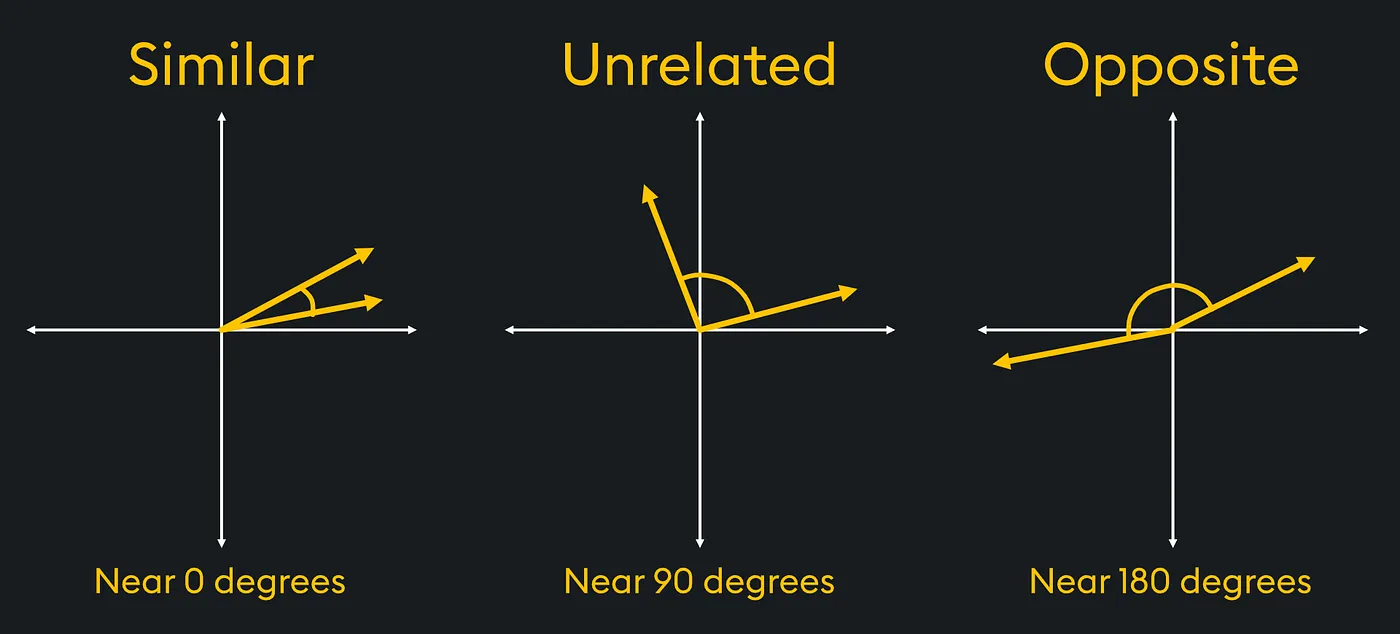
Using trigonometry we could determine which vectors are the most similar or disimilar.
Vectors in Artificial Intelligence
What should be noted is that a vector can be represented by an array of values. For three dimensions a vector is described by three points, [1, 3, 4].
In Artificial Intelligence we used arrays to represent different information in a set of data. For example if we were using Machine Learning to predict housing prices we could represent all of the information in an array.
Let’s look at a very simple example where we only have three data points to represent each house. Each element of the array would represent a different feature of the house. For example:
- Price: A dollar value.
- Number of bedrooms: Integer value.
- Size: Measured in square feet.
A hypothetical house would be represented as:
House: [300000, 3, 400]
Using our 3-dimensional housing data, we can now create an algorithm to creating a housing recommendation engine. Here are three houses represented by arrays of data:
House 1: [300000, 3, 400]
House 2: [320000, 3, 410]
House 3: [900000, 4, 630]
Plotting these three houses in three dimensions gives us the following graph.
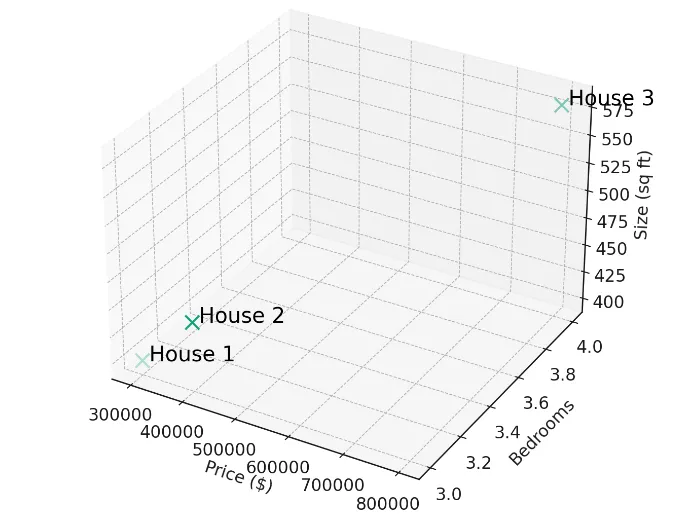
If the user wanted to find houses most similar to house 1 it can quickly be determined that house 2 is the most similar and the recommendation engine can return the details of this property to the user.
In Machine Learning the house array is referred to as a vector. What makes vectors so interesting is the same mathematics that are used on Physics vectors applies to arrays of numbers. Hence, we use the term vector.
Where it becomes impossible to visualise is when the vector contains more than three data points. A house vector could contain many data points, such as location, quality score, age, number of bathrooms etc. A complete house vector may look like this:
[300000, 3, 400, 122.2, 83.4, 87, 43, 3]
This is known as a higher-dimensional vector. In this context a dimension refers to one feature of the data. The price is a dimension. The size is another dimension and so it. Higher-dimensional vectors cannot be represented in 3-dimensional space, however, the same concepts and mathematics applies. We can still run our recommendation engine by finding the higher-dimensional vectors that are most similar.
Converting text to vectors
Where things start to get really fun for us, is when we start to convert text into vectors. The genius of modern artificial intelligence is the ability to convert words, phrases and even pages of text into a vector that represents the meaning of that information.
Let’s start with a single word, “Cat”.
Specialised AI models can take the word cat and turn it into a vector. This vector is a representation of the meaning of the word cat as it relates to other words in its training data. These specialised AIs use pre-trained models that have learned how to represent text as high-dimensional vectors. These vectors capture semantic meanings and relationships between text based on their usage within their trained data.
Converting text into vectors is known as Vector Embedding.
“Cat” might be represented by a 300-dimensional vector.
[ 0.49671415, -0.1382643 , 0.64768854, 1.52302986, -0.23415337, -0.23413696, 1.57921282, …]
“Dog” on the other hand might be represented by the vector:
[ 1.69052570, -0.46593737, 0.03282016, 0.40751628, -0.78892303, 0.00206557, -0.00089039, …]
If we were to reduce the Cat and Dog vectors into 2-dimensions it might look like this.
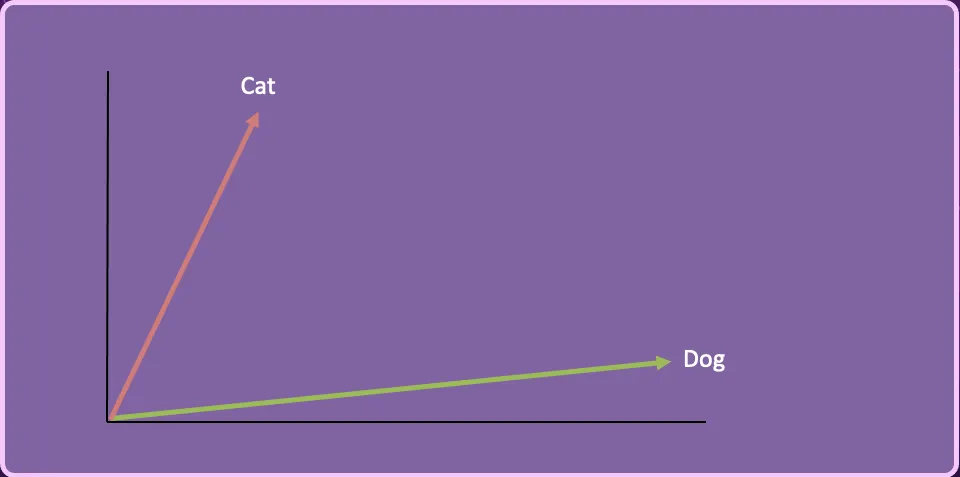
We can take a third word “Kitten”, create the vector embedding and represent it in this 2-dimensional space.
Kitten vector: [-0.05196425, -0.11119605, 1.0417968, -1.25673929, 0.74538768, -1.71105376, -0.20586438, …]
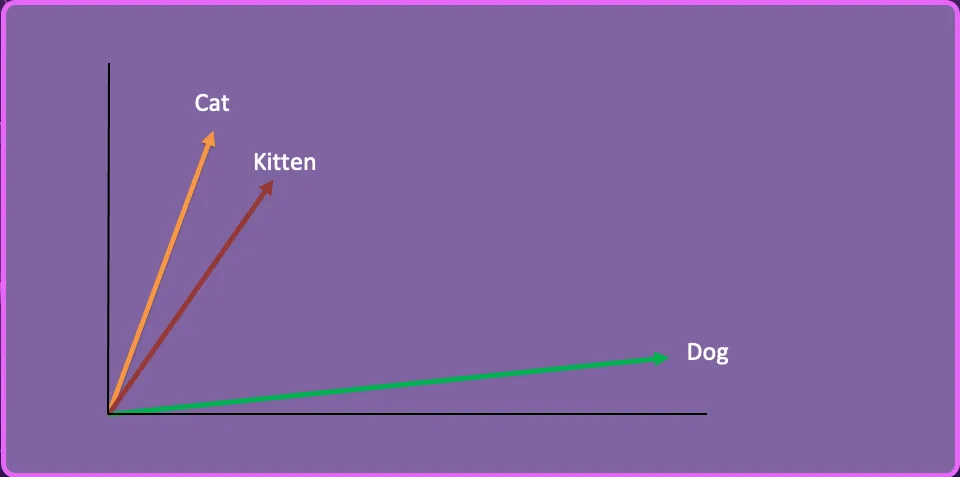
Let’s say we have a collection of articles on feeding cats and dogs, and our user asks the following question:
How do I feed my kitten?
By using similarity search, the AI determines that kitten is closer semantically to Cat than Dog and therefore returns the articles on how to feed Cats.
And this is the fundamental basis of similarity/semantic search. By converting text into vector embeddings we have a means to determine the semantic similarity to other information.
Another example might be to take the summary of a library of books and convert these into vector embeddings. The graph below shows books catelogued by genre. You will see that the books tend to cluster into groups.
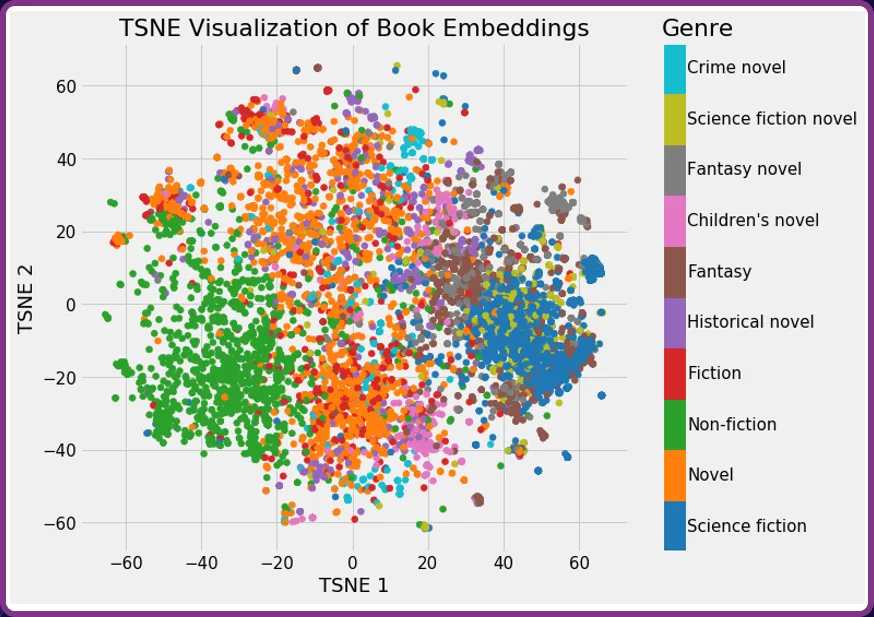
If a user were looking for recommendations on books similar to Dune, it would see Dune clustered within the ‘Science fiction’ genre and return recommendations such as ‘2001: A space odyssey’.
Creating Vector Embeddings
Vector embeddings are created by specialised AI models. OpenAI has their text-embedding-ada-002 model.
With a simple API call, text can be passed to the model which will generate a vector embedding. An OpenAI vector embedding is usually between 1500 and 3500 elements depending on the specific model used.
For information on using the OpenAI embedding endpoint check out: Open AI Platform - Embeddings
Anthropic with its Claude models also provides vector embeddings of 1024 elements: Anthrop\c Platform - Embeddings
From a programming perspective, each embedding AI model will return the vector as an array which makes it easy to work with.
Creating Vector embeddings is simply an API call away.
Storing Vector Embeddings
Vector embeddings can be stored in any type of data store. I have used CSV files during early testing (though definitely not recommended for any serious application).
There are however specialised Vector databases which have begun to emerge over the past few years. They are different from traditional databases in that they are optimised for handling vectors. These databases provide mechanisms to efficiently compute the similarity between these high-dimensional vectors.
Let’s look at what the schema of a vector database may look like. Say we are running a Fintech company with access to thousands of financial statements and we want to be able to use AI to query these documents.

This vector database has three fields:
- doc_name: The name of the document.
- doc_url: Where the original source document is stored.
- doc_vector: The vector embedding of the PDF document.
Practically every major database management system has released a version of a vector database.
PostgreSQL: They have released an extension call pgvector: pgvector, an open-source PostgreSQL
Redis: Vector Search Redis for vector database
MongoDB: Atlas vector search Atlas - Vector Search
Pinecone: A specialised vector databse Pinecone serverless lets you deliver remarkable GenAI applications faster
The choice of vector database really comes down to your development preferences.
Similarity search
Vector databases are optimised for similarity search. There are several different mathematical approaches, the most common and simplest to implement is to use cosine similarity.
Cosine similarity is a trigonometric measure used to determine how similar two vectors are. The maths determines the cosine of the angle between the two vectors. The cosine of a small angle is close to 1, and the cosine of a 90-degree angle is 0. Vectors that are very similar will have a cosine close to 1.
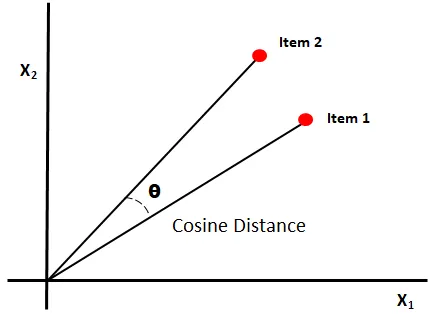
It is unnecessary to cover the mathematics of calculating cosine similarity, unless you are a maths geek like me in which case this video explains it really well: Cosine Similarity, Clearly Explained
The main take away is the closer the similarity score is to one, the more similar the vectors.
Vector databases provide functions for performing cosine similarity, where you can set parameters such as the number of results to return. For example you may want the three closest results.
Performing similarity search
Performing similarity search requires several steps.
-
Converting the source documents into vector embeddings and storing these in the vector database.
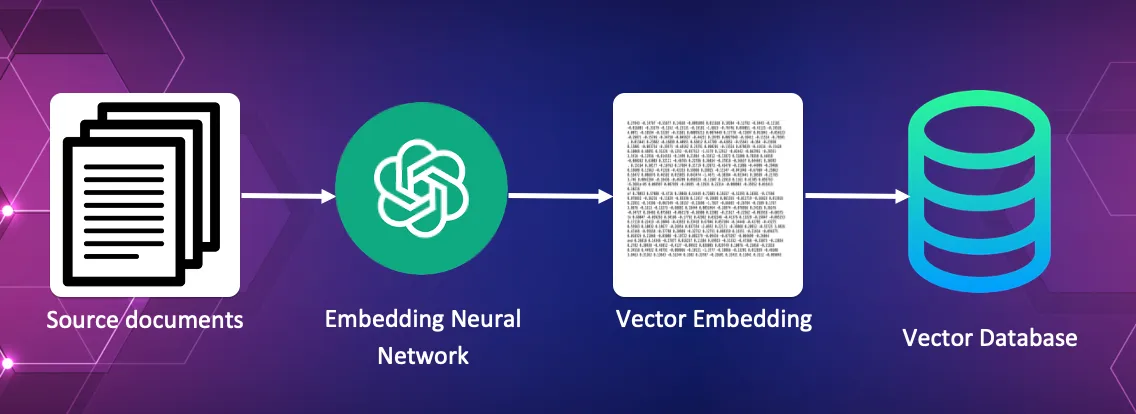
In this process each source document is feed to the embedding AI, which creates the vector embedding. These vector embeddings are then saved within the vector database along with a reference to the original source document.
For a library this might be a collection of newspaper articles from the last 100 years.
-
Converting the query into a vector and using cosine similarity to find the document most similar to the query.
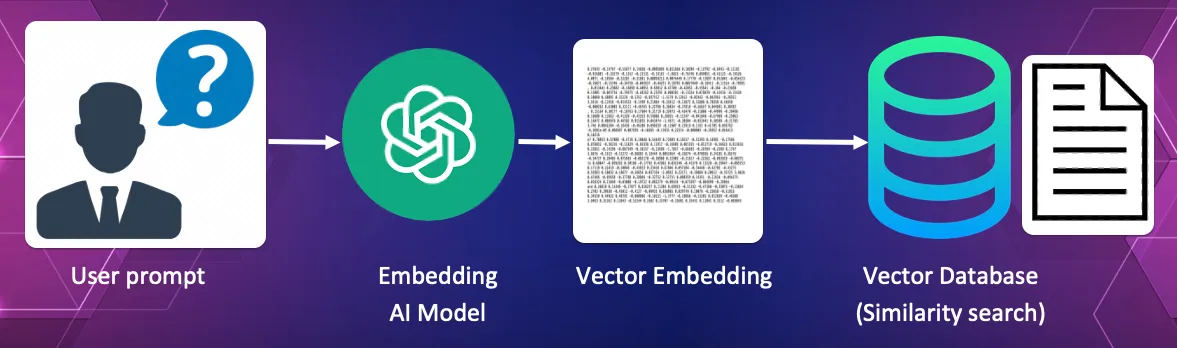
In this process the users query itself is converted into a vector. This vector is used as the search vector within the vector database to find the document which best answers the query.
For our library the query might be “I am looking for a newspaper article about the 1950 Chinchaga fire.”
This query is itself converted into a vector and passed to the vector database which uses its similarity search to find the newspaper article with the most similar meaning to the query. We may wish to return the just the top result.
The vector database will return the name of the article and the URL to the actual source text.
-
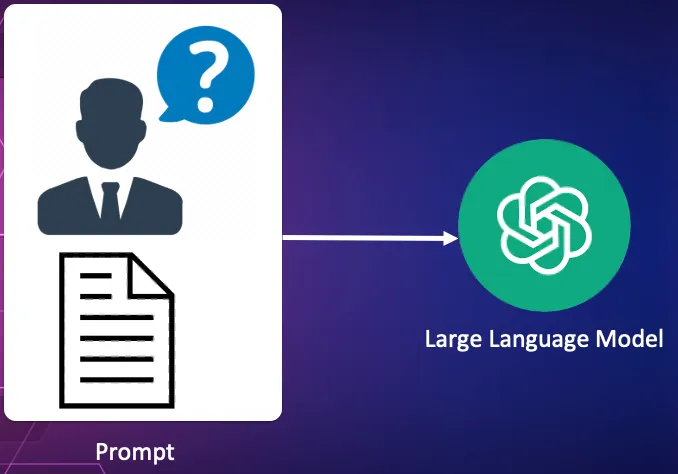
Send the query along with the source document to a LLM to verify the request.
In this process the users query itself is converted into a vector. This vector is used as the search vector within the vector database to find the document which best answers the query.
For our library the query might be “I am looking for a newspaper article about the 1950 Chinchaga fire.”
This query is itself converted into a vector and passed to the vector database which uses its similarity search to find the newspaper article with the most similar meaning to the query. We may wish to return the just the top result.
The vector database will return the name of the article and the URL to the actual source text.
-
Send the query along with the source document to a LLM to verify the request.

This is the final piece of the puzzle. The query along with the original source text is sent to a large language model to process the query against the document. The LLM used could be Claude, OpenAI, Gemini or any of the open-source models such as Llama or Mistral.
In our library example it would check that the source document actually contained information about the Chinchaga fire. If so the user would be provided with the URL to the source document.
Knowledge retrieval
This entire process is known as knowledge retrieval or Retrieval Augmented Generation (RAG).
Imagine you are working with a API for a credit card payment provider. Instead of having to trawl through API endpoints and documentation, you could just ask “What is the endpoint to process a payment?”.
The AI would used similarity search to find the correct document, and send your question and the document to an LLM. The LLM would provide an answer to the question based on the information in the source document.
You could then query further and say “How do I make this API call in Ruby?” Or JavaScript, Python, C++ etc. The LLM should be able to generate the code, based on the endpoints source documentation.
Knowledge retrieval is a very powerful means to improve the ability of users to gain access to and get answers to their exect questions without spending time reviewing the wrong informaiton.
Knowledge retrieval can be used in many way. It can be used to find and return entire articles to a user. It can find very specific information within a large source of documents. It can be used for recommendations. The use cases of knowledge retrieval just comes down to your imagination.
Knowledge retrieval as a service
Many platforms are beginning to release knowledge retrieval services, which takes the complexity and development work out of the process.
For example AWS has their Amazon Q service. Amazon Q effectively provides a point and click interface to provide it with your source documents and it will build a knowledge service for you. The beauty of Amazon Q is you can give it actual documents, store them in S3, or give it a URL and it will scrape an entire website for you. You can also have it automatically sync the data, so changes to your documents are selected within Amazon.
As we progress we will begin to see a plethora of these services.
You may have very specific use cases, where you will need to code your knowledge retrieval from the ground up. In that case you will need to work with the following tools:
- Embedding AI
- Vector database
Otherwise, your only limitation is your development skill and imagination.
Summary
Knowledge retrieval and similarity search, I believe, is the entry point to companies successful AI implementations. Where in the past keyword search was effectively mandatory for all website, we will soon see knowledge retrieval is the minimum standard. I already get frustrated when I try and work through API docs that do not have knowledge search.
I look forward to see the new and amazing ideas you come up with utilising knowledge retrieval and similarity search.
Kane Hooper is the COO of reinteractive. Learn more about Kane Hooper.
If you need any help with your AI projects you can contact Kane directly.
Ps. if you have any questions
Ask here
You may also like
The Purpose of Vector Embeddings









